Tópico: Encerrando a questão de cálculo e estatística para o passado

[Cristiano]

Segue mensagem enviada para a lista Questionando as Origens.  Basicamente é uma resposta à afirmação do Emmcri de que as chances de abiogenese ocorrer no passado são muito pequenas, logo, não ocorreu:

Bom,
quero encerrar essa falácia de se usar calculo e estatística para se calcular as chances de algo ocorrer no passado.
Na verdade, eu vou usar um exemplo que eu já mencionei aqui (um pouco alterado):

Peguemos o universo  de 180 milhões de habitantes do Brasil, onde cada habitante possui como atributos a posição X e Y em um plano de
8.547.403,5 km2 correspondendo à área total do Brasil.
Agora, com base nesses dados:
a)  calcule as chances de ocorrência de cada brasileiro estar onde estava as 14hs do dia 05/10/2005
b) calcule as chances de cada brasileiro ter estado onde esteve durante todo o dia 05/10/2005.
c) calcule as chances de cada brasileiro ter passado por onde passou durante sua vida inteira.

(Se alguem achar que estatísticas não valem para Pessoas, já que essas são inteligentes (como se tivesse alguma relação), substitua pessoas por grãos de areia ou moléculas de água.)

O que concluímos? Que as chances de algo ter ocorrido no passado são infimas... mesmo quando é um cálculo simplificado como esse que poderia ser complicado facilmente.  Segundo o Edson, já que tal coisa tem chances mínimas de ocorrer, ela não ocorre, então só posso concluir que nada ocorre no universo.  Estou errado?

Ah, eu espero que algum criacionista/DIista responda esse email com a mesma lógica com que está usando para "refutar" a abiogenese.  A mesma lógica que vocês refutam a abiogênese eu posso usar para refutar o universo.  Mas, pelo visto, tem alguém errando feio aqui.

Cientificamente, lógica não serve para determinar o que deve ou não ser pesquisado, o universo não é regido pela lógica (ainda bem!!), evidências falam mais alto.

[Huxley]

Isso que vou colocar aqui ,tb pus lá no RV:


Quanta desinformação nesse tópico.Não existe "probabilidade de eventos" para teorias científicas,muito menos para se calcular eventos singulares e muito menos ainda vários eventos singulares como essa do emmcri sugeriu.Parece complicado esses termos, mas vou por aqui um trecho dum livro que esclarecerá as coisas.A utilização de probabilidades e estatísticas em hipóteses científicas é muito diferente do que as pessoas pensam.

Vou por aqui um trecho do livro A Lógica da Pesquisa Científica de Karl Popper(p.281 a 286)

"Realmente, se tentarmos deduzir a idéia de uma probabilidade de hipóteses a uma frequência-verdade, que usa o conceito de uma sequência de enunciados, ver-nos-emos confrontados, de imediato,com a indagação: com a referência a que sequência de enunciados pode o valor de uma probabilidade a uma hípótese?[...]Um deles seria o de atribuir a hipótese determinada probabilidade-talvez não muito precisa-com base numa estimativa assentada na divisão do número de testes a que a hípótese já foi submetida pelo número de testes não-realizado.Esse caminho, contudo, também leva a nadaA estimativa a que se faz alusão pode ser calculada de modo preciso e traz como resultado igualar a probabilidade a zero.Caberia, por fim, tentar fundamentar nossa estimativa no quociente do número da divisão do número de testes que levaram a um resultado favorável pelo número de testes que levaram a um número indiferente,isto é a um resultado que não permitiu uma decisão clara[...]Esse último expediente também não leva a nada,ainda que não consideremos o fato de que,recorrendo a essa espécie de estimativa,nos afastamos muito de uma frequência-verdade e de uma probabilidade de eventos.A razão da falha dessa última tentativa está em que a definição sugerida tornaria a probabilidade de uma hipótese irremissivelmente subjetiva:a probabilidade de uma hipótese dependeria da experiência e da habilidade do experimentador e não de resultados objetivamente reproduzíveis [... ]Os enunciados básicos nunca são deduzíveis de enunciados universais apenas.Não podem estes, portanto, ser vistos como como sequências de enunciados básicos.[...]Julgo que devemos considerar totalmente fracassada a tentativa de identificar a probabilidade de hipóteses a uma probabilidade de eventos.Com efeito ambos esses tipos correspondem as pressuposições hipotéticas que por sua vez, nuca se tornam "prováveis": só podem ser corroboradas,no sentido que podem "provar sua qualidadade" sob o fogo-sob o figo de novos testes. [...]Além disso, também não sustento que as hipóteses sejam enunciados verdadeiros, mas que são apenas "conjecturas provisórias"(ou algo semelhante) e essa concepção só pode ser expressa por meio de apreciação dessas hipóteses."

Então, se pergunta, onde fica o papel para as probabilidade estatísticas na ciência?

Obviamente se utiliza mensurações de valores na ciência e elas nunca são exatas(como a constante física da carga do elétron ou a massa do próton).Quando mensurações independentes do mesmo valor entram em conflito, mas isso mão é o fim de tudo.Cientificamente a questão relevante é perguntarmos :"Comparando-se duas mensurações, quanto de discrepância seria um problema para uma teoria?" "Quanto de exatidão deve existir para ser uma confirmação forte?".Cientistas respondem estas questões utilizando probabilidades e estatísticas.É para isso que elas servem.

Quer um exemplo de utilização de estatística na evolução?

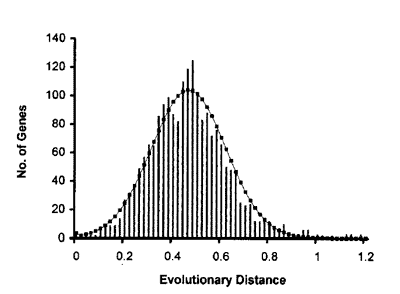
Está aqui um gráfico com a distribuição de distâncias genéticas entre o ser humano e os genes do rato. O histograma são baseado em dados reais de 2.019 genes humanos e do rato. A curva contínua mostra a distribuição prevista das distâncias genéticas que supõem uma taxa constante de mutações conhecidas(substituições ~10-9 por sítio por ano)

[APODman]

Adicionem a tudo isto os catalisadores.

Sempre esquecidos pelos Criacionistas.


[ ]´s

[Rodion]

ótimo argumento, cristiano. o outro das probabilidades já estava vencido, pra mim, mas agora ficou bem didático.