Como a Terra, só que você pode ir para "cima", saindo da esfera. Se o universo for uma esfera, eu vou retornar ao ponto que comecei se viajar sempre em linha reta, mas se eu for para "cima", caso ele não seja infinito, uma hora ou outra eu sairia do universo, assim como saímos da Terra.
Nesse tipo de analogia, você tem que ignorar o espaço ao redor da esfera (e no interior também). Uma 2-esfera (o 2 é de duas dimensões) SÓ tem superfície. É como num mapa da Terra em projeção polar: você tem que ignorar o que existe fora dos discos:
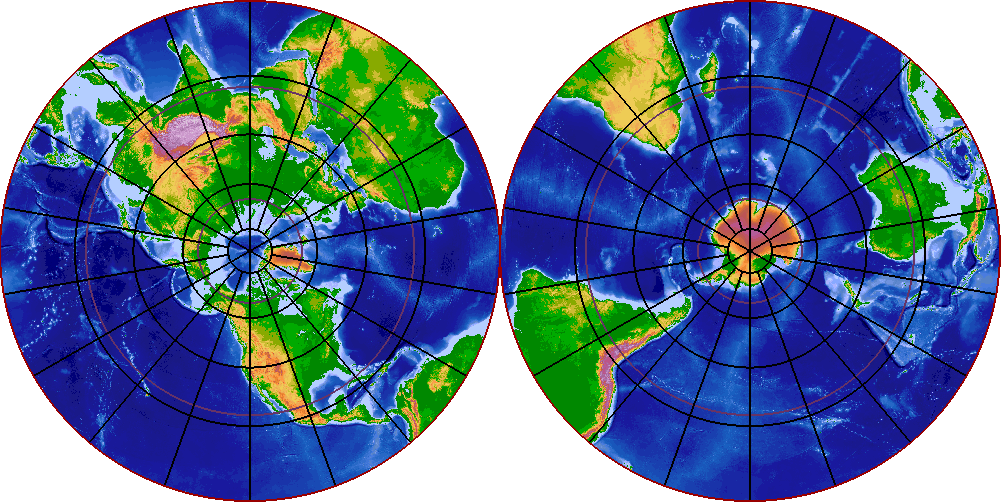
Nesse caso, a trajetória de uma pessoa viajando da Europa para o Brasil pode ser plotada como começando em um dos discos, depois "instantaneamente" passando para o outro círculo ao cruzar o equador. O espaço fora dos discos só existe para facilitar nossa visualização. Note que para uma esfera qualquer, não existe nada especial acerca dos centros dos discos. Eles podem ser escolhidos arbitrariamente (no caso do mapa da Terra é diferente, porque a rotação do planeta cria pontos especiais, os polos norte e sul). Quando a gente visualiza uma 2-esfera como um globo, estamos fazendo o que os matemáticos chamam de "embedding": estamos fazendo uma imersão de um espaço em um outro de dimensão maior.
No caso de uma 3-esfera, você pode fazer uma extensão da figura acima para uma dimensão a mais. Como antes, não há nada de especial acerca dos centros das esferas. Nesse caso, uma pessoa viajando nesse espaço atravessa o volume de uma das esferas e vai instantaneamente para o volume da outra.
Note que existem outras topologias para espaços finitos, além da 3-esfera. Um exemplo simples é o 3-toróide. Antes vamos ver como é possível descrever o 2-toróide sem fazer uma imersão em 3D: pegue uma superfície finita, como uma folha de papel, e coloque umas setas assim:
Pronto, isso é o 2-toróide! Para ver como ele fica de uma forma mais familiar, é só colar as bordas de forma que as setas iguais fiquem umas sobre as outras. Com isso (para uma folha bem flexível, na prática) temos:
No caso do 3-toróide é só ir para uma dimensão a mais:
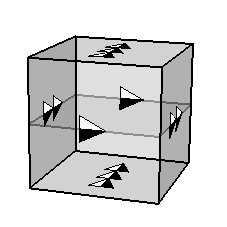
Ou seja, se você se movimentar nesse espaço, na hora em que você passar pelo "teto" da caixa, aparecerá imediatamente no "chão" dela. O mesmo vale para as outras
dimensões direções.
Para fazer uma imersão dessa figura precisaríamos de 4 dimensões, algo meio difícl de obter nesta tela, mas o importante é ver que tanto esse espaço quando o da "superfície 3D" da 3-esfera são finitos, sem bordas. A diferença entre eles é de topologia, mas aí é outra história. O legal é que um ser que habitasse um espaço finito como esse poderia descobrir, sem ir para uma dimensão maior, se vive numa 3-esfera ou num 3-toróide.
Tópico: Universo saberemos um dia a verdade??? (Lida 2767 vezes)