A rota great circle implica mudança contínua de proa (rumo).
Fui dar uma olhada agora nessa coisa de loxodromia e ortodromia que até então era idioma grego pra mim.
Você está falando com um velho marujo que já singrou destemidamente as águas turvas da baía de Guanabara a bordo de seu veleiro Optimist, um barquinho que parece um caixote de bacalhau com uma vela. Mas eu nunca precisei de bússola nem sextante em minhas aventuras marítimas e só tinha uns 10 anos na época.
Portanto fiquei confuso com essa coisa da rota "GC" precisar de mudança contínua de rumo, porque geometricamente parecia não fazer sentido.
O que parece é que esta mudança de rumo é náutica, cartográfica, porque essa rota não mantém ângulo constante com os meridianos e portanto a bússola irá indicar diferentes direções para o norte ( em relação ao barco ) durante o percurso.
Daí usarem rotas loxodrômicas, que mantém "rumo" constante. Como parece indicar a figura abaixo. ( Só lembrando que sou neófito nisso, é a 1ª vez que vejo estes termos. ).

Ou seja, a rota de "rumo" constante ( em relação ao referencial náutico ), na verdade é a que implica em mudança de rumo real.
E a rota ortodrômica, dita com correção de rumo, é aquela onde se mantém o rumo. Que é uma aparente linha reta para quem percorre a superfície do globo terrestre.
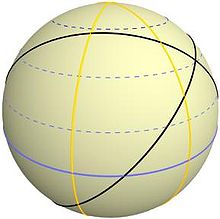
No nosso experimento mental temos que utilizar rotas ortodrômicas para traçar os catetos e hipotenusa de nosso triângulo imaginário. Quer dizer, navegamos com o leme do barco travado. Após longa distância percorrida a bússola indicaria mudança de rumo, quando na verdade estamos sempre no mesmo rumo e eventualmente retornaríamos ao mesmo ponto de partida dado uma volta inteira ao mundo.
o valor dessa correção sendo 0,57 pé multiplicado pelo quadrado da distância em milhas
Os Princípios & Prática de Agrimensura: Agrimensura avançada
por Charles Breed, 1908.
Foi bom trazer esse dado porque eu só tinha encontrado isso em uma vídeo aula de topografia, e o cara dá esses números em metros. Vou fazer a conversão e conferir pra ver se bate.
Porque esse dado é em relação a uma média, e a minha dúvida é se essa média vale pra qualquer lugar ( ex: lugares mais quentes, mais frios... ).
Porque há uma história curiosa em relação a isso: o cara que fundou a Sociedade de Astronomia Zetética e ressuscitou o mito da Terra plana no século 19, em dias de condições meteorológicas especiais, costumava levar pessoas a um canal nas proximidades de Londres e ali demonstrar que a Terra era mesmo plana.
A refração tende a curvar os raios luminosos em direção à superfície da Terra, e portanto opticamente o fenômeno atenua a percepção da curvatura. Para um determinado índice de refração a Terra parecerá efetivamente plana para uma longa distância. ( E a refração pode até fazer com que pareça côncava! )
Esse fenômeno, responsável inclusive por estranhas miragens como barcos que parecem flutuar e icebergs que são vistos a kms de onde realmente estão, é mais comum em regiões muito frias. Então o sujeito ( que agora me foge o nome ) explorava essa eventualidade para atrair incautos para a sua Sociedade Zetética.
Esse indivíduo acabou sentenciado a uma pena de prisão. Não por questionar a esfericidade do planeta, mas por fazer fortuna vendendo elixir da eterna juventude e da vida eterna para os membros da Sociedade de Astronomia Zetética.
Mais tarde um dos seus pupilos continuou ganhando dinheiro com o mesmo golpe, publicando desafios de apostas em jornais, alegando ser capaz de demonstrar ( para que se dispusesse a apostar ) que a Terra era plana. Repetindo o mesmo experimento, nesse mesmo canal.
Até que o Alfred Russel Wallace - um dos pais da Teoria da Evolução - aceitou a aposta e ficou com o dinheiro do vigarista. Apenas tomando simples providências para minimizar o efeito da refração.